Kumpulan contoh soal integral dan pembahasan yang kami sajikan pada artikel ini dikhususkan untuk siswa/siswi SMA sederajat yang memang sedang mendalami materi ini.
Harapannya dengan belajar contoh soal integral ini, pembelajaran di sekolah lebih mudah dipahami.
Untuk Anda siswa/siswi SMA, pasti sudah tidak asing lagi kan dengan pelajaran matematika dan materi tentang integral?
Nah, agar bisa memahami materi ini lebih dalam, Anda harus rajin untuk mengerjakan dan membahas contoh-contoh soal integral yang ada.
Konsep ilmu integral biasanya banyak digunakan untuk menentukan suatu luas daerah di bawah kurva, dan sering digunakan untuk mencari suatu penyelesaian dalam suatu model matematika.
Untuk memudahkan Anda belajar tentang integral, ada baiknya sudah memahami dengan baik tentang matematika dasar turunan atau diferensial karena akan digunakan dalam penyelesaian integral.
Pengertian dan Jenis Integral
Integral adalah suatu bentuk pada sebuah operasi matematika yang menjadi kebalikan atau disebut invers dari operasi turuan dan limit dari jumlah suatu luas daerah tertentu.
Integral di kategorikan menjadi 2 jenis yaitu integral sebagai invers atau integral tak tentu dan integral sebagai limit atau integral tentu.
Lebih mudahnya, integral adalah materi kalkulus dasar yang berkaitan dengan diferensial dan limit yang pada dasarnya kebalikan dari diferensial hingga disebut sebagai anti-turunan. Rumus integral tidak bisa berdiri sendiri yang artinya bergantung pada yang terdapat dalam turunan.
Diartikan sebagai kebalikan dari turunan, jika F(x) adalah fungsi umum yang bersifat F’(x) = f(x), maka F(x) adalah anti turunan atau integral dari f’(x) = f(x). Pengintegralan suatu nilai fungsi f(x) terhadap x bisa dinotasikan sebagai berikut:
∫f(x) dx = F(x) + c
Keterangan:
∫ = notasi integral
f(x) = fungsi integran
F(x) = fungsi integral yang bersifat F’(x) = f(x)
c = konstanta pengintegralan
Formula integral yang biasanya banyak digunakan adalah Integral Riemann dan rumusnya ditemukan oleh Matematikawan Jerman, Georg Friedrich Bernhard Riemann yang berbentuk:
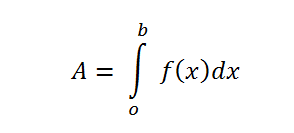
Keterangan:
A = nilai integral dari fungsi f(x)
b = batas waktu variabel yang diintegrasi
o = batas bawah variabel yang diintegrasi
f(x) = fungsi yang diintegralkan
dx = variabel yang diintegrasi
Selain rumus umum yang diketahui, terdapat 2 jenis integral yang biasa dipelajari, berikut 2 jenis integral tersebut:
1. Integral Tentu
Integral tentu adalah jenis integral yang memiliki nilai awal dan akhir, serta memiliki batas yang jelas. Biasanya bentuk interval a ≤ x ≤ b, bagian a disebut dengan batas bawah dan bagian b disebut batas atas pada sebuah integral tertentu.
Dalam aplikasinya, jenis intergal ini banyak digunakan untuk menghitung luas di bawah kurva dengan batas-batas tertentu, atau menghitung volume benda yang diputar. Rumus umum dari integral tentu sebagai berikut:
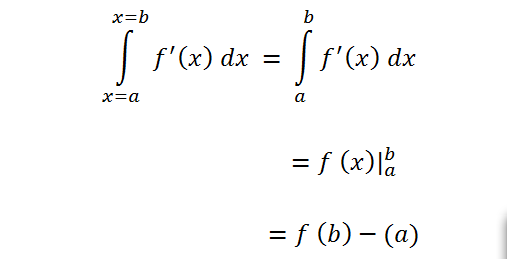
Keterangan:
x = a disebut dengan batas bawah
x = b disebut dengan batas atas
Maksud dari rumus diatas adalah nilai suatu f’(x) diintegralkan atau dijumlahkan secara kontinue, mulai dari titik a hingga ke titik b, sampai hasil akhir yang diperoleh berupa angka tidak lagi fungsi.
Sifat-sifat pada integral tentu lebih bervariasi, dalam sifat integral tentu apabila f(x), g(x) terdefinisi pada selang a, b, maka didapatkan persamaan berikut:
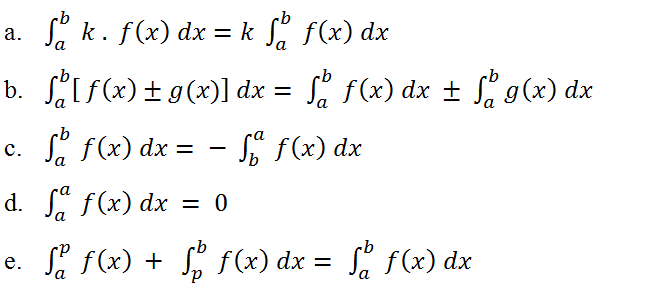
Integral ini berkaitan dengan jumlah Riemann, jumlah Riemann adalah cara untuk menghitung luas daerah yang diarsir dengan melakukan pendekatan dengan membagi daerah arsiran menjadi beberapa persegi panjang, lalu semua persegi panjang tersebut dijumlahkan.
Contoh soal integral tentu:
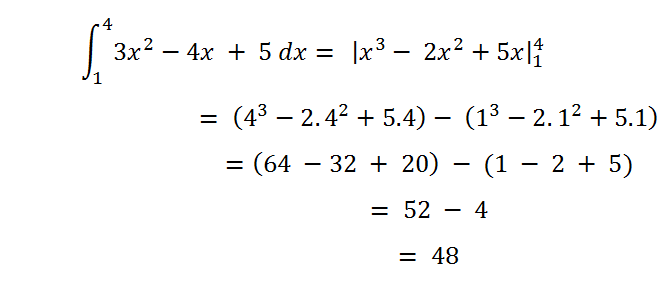
Integral tentu adalah hasil jumlahan pada suatu daerah yang dibatasi oleh kurva dari suatu persamaan tertentu.
Bedanya dengan intergal tak tentu adalah sudah memiliki nilai pasti karena batas yang ditentukan sudah jelas.
2. Integral Tak Tentu
Definisi integral tak tentu adalah suatu fungsi baru yang turunannya sama seperti fungsi aslinya, jenis ini tidak memiliki batas dan belum memiliki nilai yang jelas.
Nilai yang belum jelas tertentu dilambangkan dengan konstanta (C). Untuk lambangnya sendiri tidak memiliki batas bawah dan batas atas.
Integral tak tentu adalah bentuk operasi pengintegralan suatu fungsi yang menghasilkan fungsi baru, fungsi tersebut belum memiliki nilai pasti hingga cara pengintegralan yang menghasilkan fungsi tak tentu atau integral tak tentu.
Sebuah turunan dari suatu nilai fungsi, apabila diintegralkan akan menghasilkan sebuah fungsi sendiri. Contoh turunan dari fungsi aljabar yaitu 𝑦 = 𝑥 3 adalah 𝑦′ = 3𝑥 2 yang jika ditulis dalam integral 𝑦 = ∫ 3𝑥 2𝑑𝑥.
Beberapa kasus ditemukan bahwa banyak fungsi memiliki hasil turunan yang sama seperti contoh tersebut seperti 𝑦 = 𝑥 3 + 3 atau 𝑦 = 𝑥 3 – 10, keduanya memiliki turunan 𝑦′ = 3𝑥 2.
Jika turunan tersebut diintegralkan, seharusnya menjadi fungsi awal sebelum diturunkan. Tapi, dalam beberapa kasus tidak diketahui fungsi awal dari suatu turunan, maka hasil integral dari turunan tersebut dapat dituliskan sebagai berikut:
𝑓(𝑥) = 𝑦 = 𝑥3 + C
Dengan nilai C bisa berapapun jumlahnya, dan untuk notasi C ini biasa disebut sebagai konstanta integral.
Contoh soal integral tak tentu:
- ∫ 8x3 + 4x + 3 dx = 2x4 + 2x2 + 3x + C
- ∫ 2x (2x2 + 4) dx = ∫ (4x3 + 8x) dx
= x4 + 4x2 + C
Ada beberapa aturan yang biasanya bisa digunakan dalam penyelesaian integral:
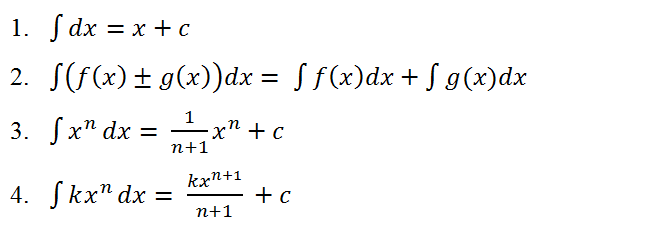
Penerapan ilmu integral sendiri dalam kehidupan sehari-hari cukup beragam, mulai dari bidang matematika, teknologi, ekonomi, fisika, teknik, kedokteran, dan lainnya.
Misalnya, dalam ilmu matematikan integral digunakan untuk menentukan luas suatu bidang, menentukan volume benda putar, dan menentukan panjang busur.
Dalam bidang ekonomi digunakan untuk, mencari fungsi asal dari fungsi marginalnya (fungsi turunannya), kemudian berguna untuk mencari fungsi biaya total, mencari fungsi penerimaan total, lalu digunakan untuk mencari fungsi konsumsi dari fungsi konsumsi marginal, fungsi tabungan dari fungsi tabungan marginal, dan fungsi kapital dari fungsi investasi.
Pada bidang teknologi, integral banyak digunakan pada kegiatan seperti, penggunaan laju tetesan minyak dari tangki untuk menentukan jumlah kebocoran selama selang waktu tertentu, pada penggunaan kecepatan pesawat ulang alik Endeavour yang berfungsi untuk menentukan berapa ketinggian maksimum yang akan dicapai pada waktu tertentu.
Bidang teknik memanfaatkan konsep integral untuk membantu para programmer dalam pembuatan aplikasi dari mesin-mesin yang handal, misalnya para engineer dalam membuat desain mesin pesawat terbang.
Kumpulan Contoh Soal Integral dan Pembahasannya
Salah satu cara agar bisa lebih memahami integral dengan baik adalah rajin mengerjakan contoh soal integral untuk memperdalam konsepnya.
Dengan banyak berlatih dan memahami konsep integral dengan baik, mudah-mudahan bisa membuat Anda lebih mengerti. Berikut beberapa contoh soal integral:
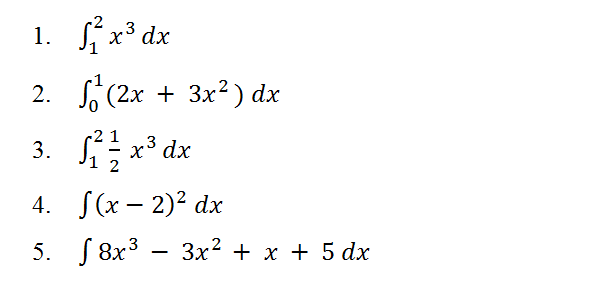
Pembahasan:
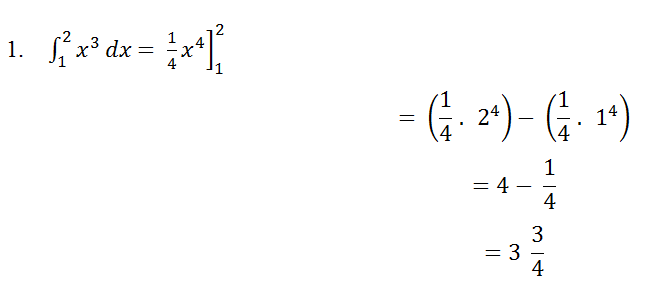
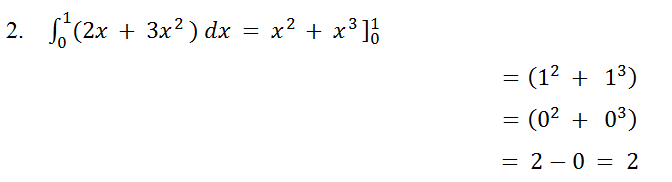
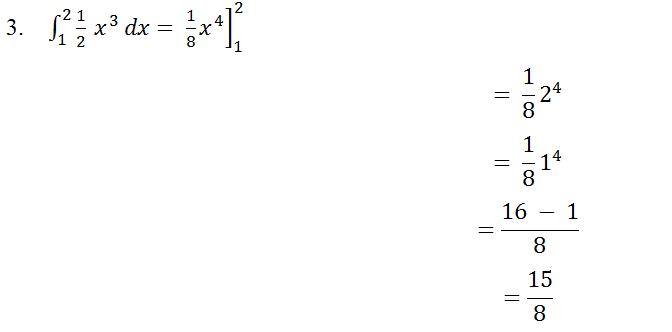
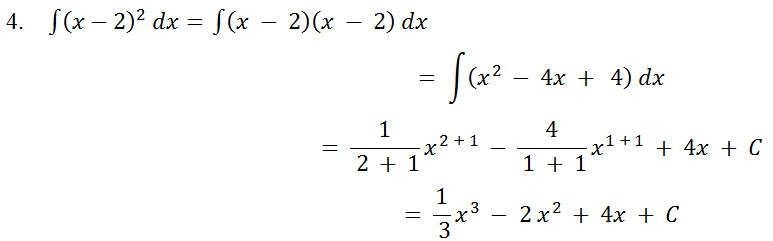
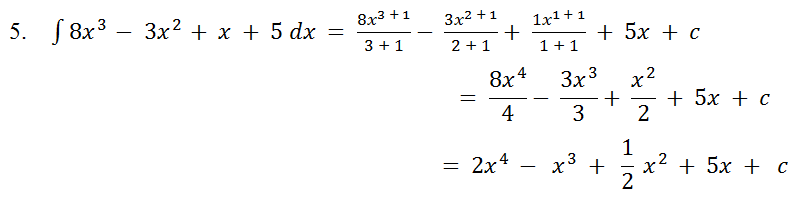
Itulah pembahasan singkat tentang integral, jenis-jenis integral yang perlu dipahami, dan contoh soal integral dengan penyelesaiannya.
Konsep integral, tanpa disadari dekat dengan kehidupan sehari-hari terutama dalam dunia kerja. Semoga ulasan dan contoh soal integral di atas bisa membantu Anda untuk lebih memahami tentang konsep dasar materi integral.