Untuk siswa SMA kelas 11, materi program linear pasti sudah tidak asing lagi karena sudah jadi sub bahasan di sekolah. Materi ini sudah dijelaskan dengan baik oleh para pengajar bahkan diberi contoh soal program linear kelas 11 agar lebih mudah untuk memahami tentang materi ini.
Saat mempelajari materi program linear, pasti dikenalkan dengan model matematika, nilai optimum, dan cara menyelesaikannya.
Tujuannya agar memperoleh perhitungan yang tepat karena berhubungan dengan biaya yang dianggarkan. Tidak hanya pengertiannya saja, nanti kita akan berikan contoh soal program linear kelas 11 yang bisa dijadikan gambaran.
Pengertian dan Model Matematikan Program Linear
Sebelum membahas lebih jauh tentang contoh soal program linear kelas 11 dan pembahasannya, kita bedah dulu apa itu program linear.
Pengertian Program Linear
Program linear adalah metode yang digunakan untuk menentukan nilai optimum suatu persoalan linear. Nilai maksimum dan minimum atau nilai optimum bisa diperoleh dari nilai suatu himpunan penyelesaian persoalan linear.
Dalam sebuah persoalan linear ada yang namanya fungsi linear yang biasa disebut dengan fungsi objektif.
Lalu apa itu fungsi objektif? Nah, fungsi objektif adalah suatu fungsi linear yang berbentuk z = f (x,y) = ax + ay, digunakan untuk mencari nilai minimum atau maksimum setelah Anda menemukan titik pojok.
Selain itu, program linear juga salah satu cara untuk menyelesaikan suatu soal yang berkaitan dengan nilai minimum dan maksimum dengan cara mengubah soal cerita menjadi sebuah model matematika.
Kemudian, akan Anda selesaikan dengan berbagai metode seperti metode garis selidik, metode uji titik pojok, dan metode gradien.
Program linear disebut juga model matematika atau bagian dari matematika terapan yang berupa pertidaksamaan maupun persamaan linear, terkadang bisa digunakan dalam kegiatan sehari-hari untuk menyelesaikan beberapa masalah.
Di ilmu matematika, program linear sendiri dinyatakan dalam bentuk kalimat pernyataan umum yang akan diubah ke dalam bentuk matematika, diubah dalam notasi matematika.
Biasanya digunakan untuk menyelesaikan masalah yang banyak berkaitan dengan nilai variabel dan ada nilai fungsi objektif yang harus dioptimalkan berdasarkan beberapa batasan.
Umumnya, penggunaanya dalam bidang bisnis yang mencari efesiensi seperti jumlah bahan bangunan maksimal yang harus dibeli dalam proses pembangunan rumah.
Di dalam kehidupan sehari-hari program linear juga banyak dijumpai seperti pada pembangunan apartemen atau perumahan.
Termasuk pada pemakaian tanah sebagai lahan parkir, pemakaian obat-obatan untuk menyembuhkan pasien, masalah transportasi, dan lainnya.
Contoh soal program linear kelas 11 yang akan kita ulas nanti di bawah ini setidaknya membahas tentang hal tersebut. Jadi, jangan lewatkan untuk coba mengerjakan contoh soal program linear kelas 11 di bawah ya.
Model Matematika Program Linear
Model matematika diartikan sebagai rumusan matematika yang diperoleh dari hasil penafsiran seseorang saat menerjemahkan masalah program linear ke dalam bahasa matematika. Model matematika dikatakan baik kalau dalam model hanya memuat bagian yang diperlukan.
Sebagai contoh soal program linear kelas 11, ada seorang siswa yang memilih jurusan IPA, jika memenuhi syarat-syarat sebagai berikut:
- Jumlah matematika dan fisika tidak boleh kurang dari 12
- Nilai pelajaran matematika dan fisika tidak boleh kurang dari 5
Buat model matematikanya agar siswa bisa memilih jurusan IPA.
Penyelesaiannya:
Misalkan: nilai matematika = x, nilai fisika = y
Jadi, untuk syarat bagian a diperoleh hubungan: x + y ≥ 12
Untuk syarat bagian b memiliki hubungan x ≥ 5 dan y ≥ 5
Maka, model matematika yang bisa Anda gunakan sebagai patokan agar siswa bisa memilih jurusan IPA adalah:
x ≥ 5 dan y ≥ 5, dan x + y≥12 ε C
Agar Anda bisa melakukan optimasi pada program linear, Anda bisa mengikut beberapa tahapan berikut:
- Menentukan variable kendala.
- Menentukan fungsi tujuan.
- Menyusun model variabel kendala.
- Menggambar grafik atas model variabel yang sudah disusun.
- Menentukan titik potong pada grafik yang sudah dibuat.
- Menentukan daerah penyelesaian.
- Menghitung nilai optimal fungsi tujuan.
Nilai Optimal Fungsi Objektif
Untuk melakukan optimasi dalam program linear adalah dengan menghitung nilai optimal fungsi tujuan. Fungsi objektif sendiri adalah fungsi linear sekaligus batasan pertidaksamaan linear dalam bentuk himpunan penyelesaian.
Suatu himpunan terdapat titik pada diagram cartesius, apabila koordinatnya disubtitusikan ke dalam fungsi linear, maka akan memenuhi syarat yang sudah ditentukan.
Agar bisa menentukan nilai optimum fungsi objektif, Anda harus menggunakan metode grafik untuk menentukan letak titik yang menjadi nilai optimum. Berikut caranya:
- Pertama kali, Anda gambar himpunan penyelesaian pada diagram cartesius.
- Kemudian, tentukan titik ekstrim dari perpotongan pada garis batas dengan garis lainnya.
- Setelah itu, Anda teliti nilai optimum menggunakan garis selidik atau membandingkan nilai fungsi pada setiap titik ekstrim.
Jika Anda menggunakan garis selidik, maka akan diperoleh fungsi f (x,y) = ax + by dan garis selidiknya ax + by = z, nilai z adalah nilai sembarang. Lalu, garis akan dibuat sesudah grafik himpunan dibuat.
Untuk menyelesaikan contoh soal program linear kelas 11 di atas, pertama Anda buat sebuah garis selidik awal pada area himpunan penyelesaian, lalu buat garis sejajar dengan garis selidik awal. Untuk memudahkan Anda menyelidiki nilai fungsi optimum, berikut cara yang bisa dilakukan:
- Cara dengan syarat a > 0
Untuk nilai maksimum, Anda harus membuat sebuah garis sejajar dengan garis awal sampai membuat himpunan penyelesaian pada bagian kiri garis. Titik yang dilalui garis adalah titik maksimumnya.
Nilai minimum, Anda susun sebuah garis sejajar dengan garis selidik awal, hingga himpunan penyelesaian di bagian kanan garis. Titik yang dilalui garis disebut dengan titik minimum.
- Cara dengan syarat b > 0
Untuk nilai maksimum, buat sebuah garis sejajar dengan garis selidik awal sampai himpunan penyelesaian terletak di bawah garis. Titik yang dilalui garis adalah titik maksimumnya.
Nilai minimum, Anda buat garis sejajar dengan garis selidik, nanti himpunan penyelesaiannya akan berada di atas garis. Titik yang dilalui garis disebut dengan titik minimum. Kalau nilainya a < 0 dan b < 0, berlaku kebalikan dari uraian ini.
Jika Anda memilih menggunakan untuk membandingkan nilai fungsi tiap titik ekstrim. Pertama-tama, Anda harus menentukan titik potong garis batas, titik tersebut adalah nilai ekstrim, berpotensi mempunyai nilai maksimum di salah satu titiknya.
Dari titik tersebut, titik akan ditentukan nilai setiap fungsi dan Anda bandingkan. Nilai terbesarnya disebut nilai maksimum dan nilai terkecil disebut nilai minimum.
Contoh Soal Program Linear Kelas 11 dan Pembahasannya
Sebelum dibahas contoh soal program linear kelas 11, untuk mempermudah pekerjaan menjadi lebih sistematis, berikut tahapan bagaimana menentukan nilai optimum dari fungsi objektif atau fungsi tujuan.
Tentukan DHP
Langkah pertama untuk menentukan nilai optimum dari suatu fungsi objekif, Anda harus sudah menentukan daerah himpunan penyelesaian.
Cari Titik Pojok
Setelahnya, Anda mulai cari titik pojok pada DHP dengan menggunakan sistem persamaan linear dua variabel atau SPLDV untuk mencari titik pojok yang belum diketahui.
Baca juga: Contoh Soal Aljabar Kelas 7 dan Cara Penyelesaiannya
Mencari nilai optimum
Kemudian, Anda bisa mulai mencari nilai optimum dengan cara memasukkan setiap pojok kepada fungsi tujuan,
Dalam program linear, nilai paling besar akan disebutkan nilai maksimum, dan titik pojok disebut sebagai titik maksimum. Nilai paling kecil akan disebut dengan nilai minimum dan titik pojoknya dibilang titik maksimum.
Berikut ada contoh soal program linear kelas 11 yang bisa menjadi salah satu bahan belajar untuk Anda:
- Seorang pedagang memproduksi dua jenis kue. Setiap kue jenis 1 modalnya Rp 2.000, sedangkan kue jenis 2 modalnya Rp 3000. Modal yang tersedia adalah Rp 1.000.000, dan paling banyak yang bisa memproduksi 500 kue. Model matematika dalam soal ini adalah?
- Sebuah perusahaan mebel memerlukan sekita 18 unsur A dan memerlukan sekitar 24 unsur B per hari. Untuk barang jenis I dibutuhkan 1 unsur A dan 2 unsur B, sedangkan untuk membuat barang jenis II dibutuhkan 3 unsur A dan 2 unsur B. Barang jenis I dijual dengan harga Rp 250.000 per unit, barang jenis II dijual dengan harga Rp 400.000 per unit. Supaya penjualan mencapai maksimum, berapa banyak barang yang harus dibuat dari jenis I dan jenis II adalah?
Penyelesaian:
Penyelesaian dari contoh soal program linear kelas 11 di atas adalah sebagai berikut:
1. Misalkan: kue jenis 1 adalah x dan kue jenis 2 adalah y
Paling banyak hanya bisa memproduksi 500 kue x + y = 500
Modal yang tersedia adalag Rp 1.000.000
2000x + 3000y ≤ 1000.0000
2x + 3y ≤ 1000
2. Misalkan: barang jenis I adalah x dan barang jenis II adalah y
| Jenis Barang | Unsur A | Unsur B | Harga |
| I | 1 | 2 | Rp 250.000 |
| II | 3 | 2 | Rp 400.000 |
| Jumlah | 18 | 24 |
Fungsi tujuan: f (x,y) = 250.000 + 400.000
Fungsi Kendala: x + 3y ≤ 18
2x + 2y ≤ 24 atau x + y ≤ 12
x ≥ 0, y ≥ 0
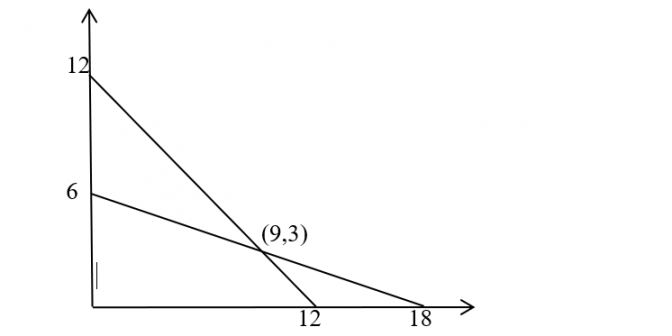
Menentukan titik potong fungsi kendala:
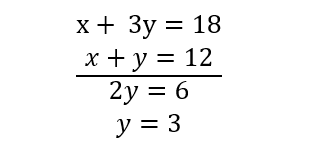
Subtitusi y = 3 ke persamaan x + y = 12 dan diperoleh
x + y = 12
x = 9
| Titik Sudut | f (x,y) = 250.000x + 400.000y | ||
| 12,0 | 250.000 (12) | 400.000 (0) | 3.000.0000 |
| 9,3 | 250.000 (9) | 400.000 (3) | 3.450.000 |
| 0,6 | 250.000 (0) | 400.000 (6) | 2.400.000 |
Jadi, penjualan mencapai maksimum saat titik sudut (9,3) yang berarti banyak barang jenis I yang harus dibuat 9 dan barang jenis II 3.
Demikian ulasan singkat mengenai program linear dan contoh soal program linear kelas 11 yang bisa menjadi salah satu referensi Anda untuk belajar. Semoga pembahasan mengenai beberapa contoh soal program linear kelas 11 di atas mudah untuk dipahami. Selamat belajar.